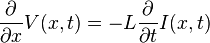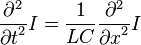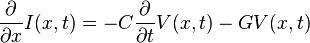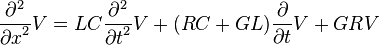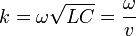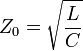HISTORIAS DEL TELEGRAFISTA

eCUACIONES DEL TELEGRAFISTA!!!

Oliver Heaviside desarrolló un modelo matemático de línea de transmisión, conocido como ecuaciones del telégrafo, que describe la variación instantánea de la tensión y corriente eléctricas a lo largo de un conductor.

La teoría fue desarrollada para las líneas de transmisión de comunicaciones, como los hilos telegráficos y los conductores de radiofrecuencia; sin embargo, también es aplicable en su totalidad al diseño de las líneas de transmisión de potencia. Las ecuaciones constan de dos ecuaciones diferenciales lineales en función de la distancia y el tiempo: una para V(x, t) y otra para I(x, t). El modelo demuestra que la energía eléctrica puede reflejarse en la línea, y que se podían formar patrones de onda conocidos.

[editar]Ecuaciones

Las ecuaciones del telégrafo pueden entenderse como una simplificación de las ecuaciones de Maxwell. Para fines prácticos, se asume que el conductor está compuesto por una serie de redes bipuerto (cuadripolos) elementales, representando cada cual un segmento infinitesimal de la línea de transmisión. Un segmento infinitesimal de línea de transmisión queda caracterizado, por cuatro parámetros distribuidos, conocidos también habitualmente como parámetros primarios de la línea de transmisión.

La inductancia distribuida (expresada en henrios por unidad de longitud) debido al campo magnético alrededor conductor, se representa como una sola bobina en serie L. El parámetro L modela el proceso de almacenamiento energético en forma de campo magnético que se produce en la línea.
El comportamiento capacitivo distribuido (expresado en faradios por unidad de longitud) debido al campo eléctrico existente en el dieléctrico entre los conductores de la línea, se representa por un solo condensador en paralelo C, colocado entre "el conductor de ida" y "el conductor de retorno". El parámetro C modela el proceso de almacenamiento energético en forma de campo eléctrico que se produce en la línea.
La resistencia distribuida en el conductor (expresada en ohmios por unidad de longitud) se representa por un solo resistor en serie R. Este parámetro modela la disipación de potencia debido a la no idealidad de los conductores (pérdidas óhmicas).
La conductancia distribuida (expresada en mhos por unidad de longitud o siemens por unidad de longitud) se representa por una conductancia en paralelo G, colocada entre "el conductor de ida" y "el conductor de retorno". El parámetro G modela la disipación de potencia que se produce por la no idealidad del medio dieléctrico (pérdidas dieléctricas).

Cuando los parámetros R y G son muy pequeños, sus efectos se pueden ignorar, de manera que la línea de transmisión se puede considerar una estructura ideal y sin pérdidas. En este caso, el modelo depende sólo de los parámetros L y C, de los cuales obtenemos un par de ecuaciones diferenciales parciales, una de ellas para la tensión y otra para la corriente, a través de la línea, ambas en función de la posición o distancia x y del tiempo t.

$\frac{\partial}{\partial x} V(x,t) = -L \frac{\partial}{\partial t} I(x,t)$

$\frac{\partial}{\partial x} I(x,t) = -C \frac{\partial}{\partial t} V(x,t)$

Estas ecuaciones pueden combinarse para formar cualquiera de estas ecuaciones de onda exactas:

$\frac{\partial^2}{{\partial t}^2} V = \frac{1}{LC} \frac{\partial^2}{{\partial x}^2} V$

$\frac{\partial^2}{{\partial t}^2} I = \frac{1}{LC} \frac{\partial^2}{{\partial x}^2} I$

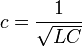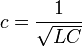Si la línea posee una longitud infinita o está terminada en su impedancia características, estas ecuaciones nos indicarán además la presencia de una onda que viaja con velocidad $c = \frac{1}{\sqrt{LC}}$ .

(Nótese que esta velocidad de propagación sólo es aplicable a la onda y no tiene nada que ver con la velocidad de arrastre del electrón, caso aparte para el cual existen otras ecuaciones y otra teoría. Para una línea de transmisión lineal homogénea e isótropa, hecha de conductores perfectos y con vacío entre ellos, se puede demostrar que dicha velocidad es igual a la de la luz.)

[editar]Línea de transmisión disipativa

Cuando las pérdidas por disipación en los elementos R y G no son despreciables, las ecuaciones diferenciales originales que describen el cuadripolo elemental pasan a tener la forma

$\frac{\partial}{\partial x} V(x,t) = -L \frac{\partial}{\partial t} I(x,t) - R I(x,t)$

$\frac{\partial}{\partial x} I(x,t) = -C \frac{\partial}{\partial t} V(x,t) - G V(x,t)$

Derivando la primera ecuación respecto de x y la segunda respecto de t, obtendremos, con ayuda de manipulación algebraica, un par de ecuaciones diferenciales parciales hiperbólicas de sólo una incógnita:

$\frac{\partial^2}{{\partial x}^2} V = L C \frac{\partial^2}{{\partial t}^2} V + (R C + G L) \frac{\partial}{\partial t} V + G R V$

$\frac{\partial^2}{{\partial x}^2} I = L C \frac{\partial^2}{{\partial t}^2} I + (R C + G L) \frac{\partial}{\partial t} I + G R I$

Nótese que las ecuaciones se parecen mucho a la ecuación de onda homogénea con términos adicionales en V e I y sus primeras derivadas. Estos términos adicionales en la ecuación son, físicamente, el efecto que causa el decaimiento (atenuación) y distorsión de la señal en la distancia y el tiempo.

[editar]Dirección de propagación de la señal

Las ecuaciones de onda indicadas líneas arriba nos muestran dos soluciones posibles para la onda viajera: una onda incidente (o progresiva) y una onda reflejada (o regresiva).

$V(x,t) \ = \ f_1(\omega t-kx) + f_2(\omega t+kx)$

donde

$k = \omega \sqrt{LC} = {\omega \over v}$

se llama número de onda y posee unidades de radianes por metro,

ω es la frecuencia angular o natural, en radianes por segundo,

$f_1$ y $f_2$ pueden ser cualesquiera funciones imaginables, y

$v = { 1 \over \sqrt{LC} }$

representa la velocidad de propagación de la onda.

$f_1$ representa una onda viajera según la dirección positiva de x, mientras que $f_2$ representa una onda viajera según la dirección negativa de x. Se puede decir que la tensión instantánea en cualquier punto x de la línea, V(x), es la suma de las tensiones de ambas ondas.

Dado que la corriente I guarda relación con la tensión V en las ecuaciones del telégrafo, podemos escribir

$I(x,t) \ = \ { f_1(\omega t-kx) \over Z } - { f_2(\omega t+kx) \over Z }$

donde

$Z_0 = \sqrt { {L \over C} }$

es la impedancia característica (en ohmios) de la línea de transmisión.

Video del telegrafo!!!!

EL TELEGRAFO!!!!!

El telégrafo es un dispositivo de telecomunicación destinado a la transmisión de señales a larga distancia. El de más amplio uso a lo largo del tiempo ha sido el telégrafo eléctrico, aunque también se han utilizado telégrafos ópticos de diferentes formas y modalidades funcionales.

El 6 de mayo de 1833, el fransiscano, astrónomo y físico alemán Johann Carl Friedrich Gauss y su amigo, Wilhelm Eduard Weber, instalaron una línea telegráfica de 1000 metros de longitud sobre los tejados de la población alemana de Göttingen donde ambos trabajaban, uniendo la universidad con el observatorio astronómico. Este dispositivo fue inventado por el estadounidense Samuel Morseen 1832. Al principio, el sistema carecía de un código para la comunicación, pero pronto ambos crearon un alfabeto basado en la amplitud de las señales dándole así una verdadera capacidad de comunicación a su invento.

Cuando en la estación emisora se cierra el interruptor, comúnmente llamado manipulador, circula una corriente desde la batería eléctrica hasta la línea y el electroimán, lo que hace que sea atraída una pieza metálica terminada en un punzón que presiona una tira de papel, que se desplaza mediante unos rodillos de arrastre, movidos por un mecanismo de relojería, sobre un cilindro impregnado de tinta, de tal forma que, según la duración de la pulsación del interruptor, se traducirá en la impresión de un punto o una raya en la tira de papel. La combinación de puntos y rayas en el papel se puede traducir en caracteres alfanuméricos mediante el uso de un código convenido, en la práctica el más utilizado durante muchos años ha sido el código Morse.

Posteriores mejoras de los dispositivos emisores y transmisores han permitido la transmisión de mensajes de forma más rápida, sin necesidad de recurrir a un manipulador y a la traducción manual del código, así como el envío simultáneo de más de una transmisión por la misma línea. Uno de estos dispositivos telegráficos avanzados es el teletipo, cuyo modelo inicial era una máquina de escribir especial que transmitía como señales eléctricas las pulsaciones sobre un teclado, mientras imprimía sobre un rollo de papel o hacía perforaciones en una cinta también hecha de papel. Las formas más modernas de esta máquina se fabricaron con un monitor o pantalla en lugar de una impresora. El sistema todavía es utilizado por personas sordas o con serias discapacidades auditivas, a fin de enviar mensajes de texto sobre la red telefónica.

La necesidad de codificar el texto en puntos y rayas para transmitirlo y descodificarlo antes de escribir el telegrama llevó al desarrollo de otros tipos de telegrafía que realizaran estas tareas de forma automática. El telégrafo de Huygens se basa en dos ruedas que contienen todos los símbolos o caracteres que se pueden transmitir y giran, sincronizadas, a la misma velocidad. Entonces, si en la rueda del transmisor tiene, digamos, la C abajo, el receptor también. Esto permite que, transmitiendo un pulso en el momento adecuado, el receptor imprima el carácter correspondiente. Como la velocidad de la transmisión depende del número de símbolos disponibles, éstos están separados en dos bancos (letras y números), de modo que comparten el mismo código una letra y un número. Existen dos blancos o espacios, llamados "blanco de letras" y "blanco de números", que además de crear un espacio para separar las palabras o los números, indican si a continuación se transmitirán letras o números. El transmisor tiene un teclado, semejante a un piano, con los caracteres. El radiotelegrafista pulsa la tecla adecuada y, cuando la rueda que contiene los caracteres está en la posición adecuada, el aparato transmite un pulso a la línea. En el receptor, un electroimán golpea la cinta de papel contra la rueda que contiene los tipos. Estas ruedas se mueven mediante un mecanismo de relojería, con motor de pesas o hidráulico, según los casos. Al comienzo del día se iniciaba un protocolo de sincronización, transmitiendo un mensaje diseñado a tal efecto. La velocidad de transmisión era inferior a la del sistema Morse, y dependía del radiotelegrafista, ya que uno experimentado era capaz de enviar varios caracteres en un giro de la rueda.

Aunque Inglaterra inició la ingeniería con cables submarinos, el empresario estadounidense Cyrus W. Field persistió haciendo esfuerzos que por fin resultaron en tender el primer cable atlántico que dio buenos resultados. Al fin y al cabo, llegó a ser un esfuerzo unido de los gobiernos de Inglaterra y los Estados Unidos. De ambos lados algunos de los financieros, oceanógrafos, telégrafos y científicos más célebres del mundo colaboraron en esta empresa. Los talentos de estos hombres resultarían indispensables debido a las profundas fosas submarinas que se encontrarían en medio del Atlántico. Aquí la cordillera más grande de la Tierra se extiende por 1.600 kilómetros de longitud y 800 kilómetros de ancho, completamente sumergida.

Si Field y sus asociados hubiesen sabido de antemano de los muchos años de problemas financieros y desastres que les esperaban al colocar el cable, es muy posible que se hubieran retirado durante sus primeros esfuerzos. Los destrozos de cable, el tiempo adverso y los enredos del cable en el aparato de arriarlo de los barcos constantemente impedían el proyecto. A veces cientos de kilómetros de cable roto, cuyo costo ascendía a una fortuna, fueron abandonados en el fondo del mar.

Era preciso resolver el viejo problema del retardo de las señales. Alguien tenía que descubrir cuánto tardaría una señal en llegar a los extremos lejanos del cable y cuántaelectricidad se necesitaría para llenar el cable antes que la señal pudiera pasar. Se ha comparado esto a un tubo de agua. Cierta cantidad de agua tiene que fluir por el tubo antes que se pueda ver una cantidad notable al otro extremo. Se puede requerir hasta 20 veces más electricidad para cargar un cable submarino que uno aéreo. Sir William Thomson, (más conocido como lord Kelvin) escribió su famosa “Ley de los Cuadrados” como resultado de su investigación de este mismísimo asunto. Simplificada, su ley quiere decir que si se multiplica 10 veces la longitud de un cable sumergido, la velocidad de la señal será reducida 100 veces. La solución que él presentó fue aumentar el tamaño del centro conductor. No obstante, debido a que se pasó por alto este nuevo descubrimiento, el diseño defectuoso del primer cable atlántico contribuyó a su subsiguiente fracaso.

Pero, por fin, el 5 de agosto de 1858 el primer cable submarino trasatlántico unió los continentes entre Irlanda y Terranova. Once días más tarde, un mensaje de saludos de 99 palabras de la reina Victoria de Inglaterra al presidente Buchanan de los Estados Unidos empezó a pasar por las líneas. Fue completado 16 1⁄2 horas más tarde. Lamentablemente, el cable falló menos de un mes después. Al costo actual, cerca de dos millones de dólares de capital privado quedaron hundidos en las profundidades del Atlántico. Lo que se había llamado “el mayor logro del siglo” se había desplomado. Ocho años pasarían antes que los europeos y americanos volvieran a hablar por alambres.

Durante el ínterin, los dos fabricantes de cables de Inglaterra se unieron, resolviendo así muchos de los problemas más tempranos de la construcción de cables. Se diseñó un cable nuevo y mejor protegido. Era dos veces más pesado (6.350 toneladas) y tenía un centro conductor tres veces más grande que el cable anterior. Podía colgar verticalmente en el agua por 16 kilómetros antes de quebrarse. Y para el siguiente esfuerzo solo tuvo que usarse un barco (en vez de los dos que se requerían antes) porque éste era capaz de llevar la tremenda carga. Esta embarcación, el Great Eastern, tenía un sistema de propulsión doble de dos ruedas de paletas de 18 metros, seis mástiles, y una hélice de siete metros. Esto hizo de ella la nave de mayor maniobrabilidad construida hasta la fecha. Por medio de dar marcha atrás a una sola rueda, la nave podía hacer un giro completo sobre su propio eje.

Después de otros dos esfuerzos infructuosos, el 27 de julio de 1866¹ ² se completó un cable que verdaderamente tuvo éxito. Este unió a Irlanda con Terranova. Pero una distancia de 1.100 kilómetros del cable nuevo yacía otro enredado con los arpeos que se habían perdido... una víctima del fracaso del verano anterior. Después de 30 esfuerzos, lograron halarlo a la superficie, someterlo a pruebas y empalmarlo con cable nuevo. Esto completó la porción de occidente a oriente. Con la unión de los extremos de los dos cables en Terranova, llegó a existir un circuito submarino de más de 6.400 kilómetros. Se enviaron señales claras a través de esta distancia. Lo único que se necesitaba para cargar este cable era una batería simple hecha de un dedal de plata que contenía unas cuantas gotas de ácido. Desde ese tiempo, la comunicación de dos direcciones entre los doscontinentes nunca ha cesado por más de unas cuantas horas a la vez.

PARA QUE ESTO????

Primero que nada este blog se creo para cumplir con una tarea que fue solicitada en el curso de TICs del diplomado de PIME en la UACJ,!!!!!!!

sábado, 12 de mayo de 2012